Approximation of High-Dimensional Non-Convex Feasible Regions

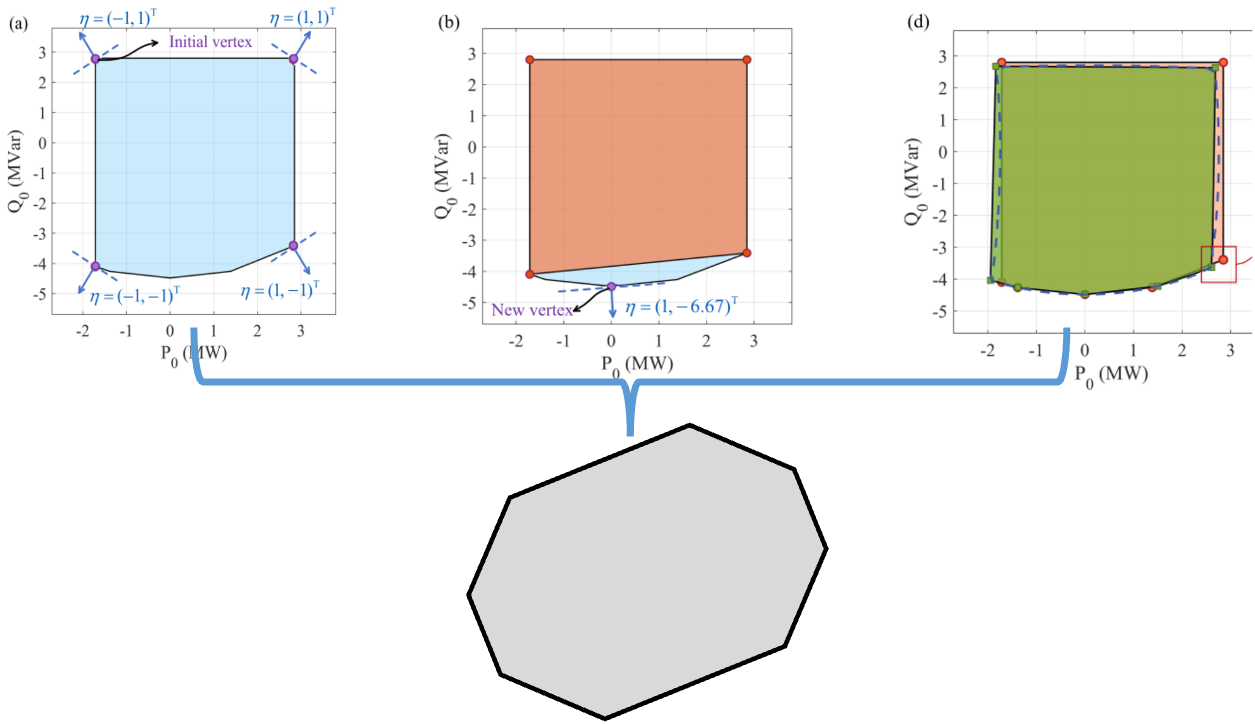
The Scientific Challenge

Approximating high-dimensional, non-linear, and non-convex feasible regions with simpler, low-dimensional constraints is a classic scientific challenge. This problem is closely related to the Minkowski sum (the sum of several sets), which mathematicians have recognized as exceptionally difficult for hundreds of years.

This challenge becomes critically important in power systems when managing interactions between demand-side resources and the power grid. In each province of China alone, there can be tens of thousands of industrial users at high voltage levels and millions of users at low voltage levels. To enable effective interaction, we need to model their collective feasible region or flexibility without causing economic losses. However, representing this information with the original high-dimensional constraints would be computationally intractable.

Limitations of Existing Approaches

Previous research has used analytical methods to approximate the feasible regions of flexible resources. However, these approaches have significant limitations:

1. Limited adaptability: They only work for resources that can be described with convex feasible regions
2. Incompatibility with integer variables: They cannot handle industrial users with integer variables, even after minimization techniques are applied
3. Unnecessary conservation: In practical grid interactions, some degree of error is acceptable, as markets can still function and demand-side resources can still receive compensation

Our Data-Driven Approach

Considering these challenges, we developed a novel data-driven method to approximate feasible regions. Compared to analytical methods, our approach:

• Is adaptable to all types of loads, not just industrial loads
• Solves the sampling problem for temporarily coupled constraints
• Uses data-driven inverse optimization rather than classical machine learning classifiers
• Includes practical algorithms for implementing the training process

The results are impressive: our method can accurately approximate loads with different models and parameters using the same input-output interface, making it highly versatile and practical.

Research Publications

Our work in this area includes:

1. Analytical Methods: We explored analytical approaches for industrial load feasible region calculation, published as a Chinese journal papers

2. Initial Data-Driven Applications: We first applied data-driven methods to electric vehicles in a PES General Meeting conference paper. Codes

3. Industrial Load Application: We recently published a paper in IEEE Power & Energy Letters applying this approach to industrial loads. Codes Explanation Video

4. Mining Industry Case Study: For the 2025 PES General Meeting, we have submitted a paper using our method in mining applications.

Impact and Applications

This research addresses a fundamental computational challenge in integrating massive numbers of flexible resources into power systems. By providing an efficient way to approximate complex feasible regions, we enable:

• Scalable integration of industrial users in electricity markets
• Computationally tractable optimization for large-scale demand response
• More accurate representation of demand-side flexibility in power system operations
• Better coordination between grid operators and flexible resources

Our data-driven approach represents a significant advancement in the field, making previously intractable problems solvable within acceptable error bounds for practical applications.